LA PASCUA DE RESURRECCIÓN
PASCUA JUDÍA:
Fiesta anual solemne celebrada por los judíos para celebrar su liberación de Egipto. La narración bíblica muestra a Moisés ordenando a cada familia hebrea que inmolara al anochecer un cordero , que tiñera con sangre el dintel de la puerta de la casa para que sus hijos no fueran inmolados como los de los egipcios y que lo comieran vestidos de viaje.
Jesucristo instituyó la Eucaristía durante la celebración de la Pascua Judía. Según tradición la Pascua Judía tenía lugar la noche del plenilunio (luna llena) del 14 al 15 del mes judío Nisan, primer mes de la primavera, (marzo o abril del calendario gregoriano). La fecha de la Pascua, al ser el calendario judío lunisolar, depende pues, del movimiento de la Luna.
PASCUA CRISTIANA:
Es el domingo con el que concluye la Semana Santa y en el que se conmemora la muerte y Resurrección de Jesucristo. Es la fiesta más importante del año litúrgico y el centro mismo del culto cristiano.
Según tradición cristiana Jesucristo murió el viernes y resucitó el domingo, día 16 del mes Nisán del año judío (según algunos correspondería al 9 de abril del año 30 en el calendario juliano).
La Pascua resulta de una adaptación al cristianismo de una ancestral fiesta pagana de carácter estacional. El comienzo de las estaciones ha sido motivo de celebraciones desde tiempos prehistóricos. En nuestra civilización el cristianismo procuró adaptar estas fiestas al cristianismo: Navidad (comienzo del invierno), Pascua (de la primavera), San Juan Bautista (del verano).
DIA DE CELEBRACIÓN DE LA PASCUA CRISTIANA:
 |
|
Domingo de Pascua en Catí (Castellón- España)-04-04-2010 |
A lo largo de la historia la Pascua Cristiana se ha celebrado utilizando diferentes criterios según la época:
Del año 30 DJC al 325 DJC: Al principio la Pascua Cristiana se celebraba haciéndose coincidir con la Pascua Judía, dia 14 del plenilunio, independientemente del día de la semana que cayese. Poco a poco se fue imponiendo la costumbre de celebrar la pascua cristiana el domingo posterior al dia de la Pascua Judía.
Del 325 DJC al 1582 DJC: A partir del Concilio de Nicea (año 325 DJC), la Pascua Cristiana paso a celebrarse el domingo siguiente al XIV día de la primera luna llena (plenilunio) después del equinoccio de primavera en el Hemisferio Norte, que coincide con el 21 de marzo o es inmediatamente posterior (se buscó una fórmula que no dependiera exclusivamente de la Pascua Judía).
![]()
![]()
El Domingo de Pascua es el primer Domingo después
de la Luna Llena posterior al 21 de Marzo
Del 1582 DJC al 4099 DJC: A partir del 4 de octubre de 1582 fue introduciéndose en la mayoría de los países el calendario gregoriano para sustituir al calendario juliano. La Pascua, no obstante continuó celebrándose en el domingo del primer plenilunio de primavera en el Hemisferio Norte pero ya del nuevo calendario gregoriano.
Sin embargo en algunas comunidades cristianas ortodoxas de países del este, que obtuvieron su autonomía el año 1504, se continuó tomando como base el calendario Juliano para celebrar la Pascua hasta la actualidad.
A partir del año 6400 será necesario volver a hacer una nueva corrección en un día en el calendario gregoriano.
Como vemos, y como era de prever por el contexto de la época, se utilizó
el ciclo lunar que es de 29-30 días, y la regla establecida desde el siglo IV
para toda la cristiandad y que aún pervive, fijó que la fiesta de la Pascua de
Resurrección, debe celebrarse el primer domingo que sigue a la catorce noche, de
lunación. Cómo el primer día de ésta lunación se sitúa necesariamente entre el 8
de Marzo y el 5 de Abril, la Pascua puede caer lo más pronto el 22 de Marzo y
cómo más tarde, en principio y sólo en principio, el 18 de
Abril, un intervalo de 35 días.
Calculándolo de otra manera:
20+29=49;
49-31=18
20 de Marzo (último día de invierno) + 29 (ciclo lunar) =49. 49
de Marzo que dicho de otra manera es el 18 de Abril, ya que 49-31=18. Fecha más
tardía como se ha dicho.
Y decíamos que en principio y sólo el principio; ya que no se quiso, para evitar confusiones, que aunque fuese en caso extremo, pudiera coincidir la celebración de la Resurrección con la festividad judía; por lo que se le añadió a este período una semana más, hasta el 25 de Abril.
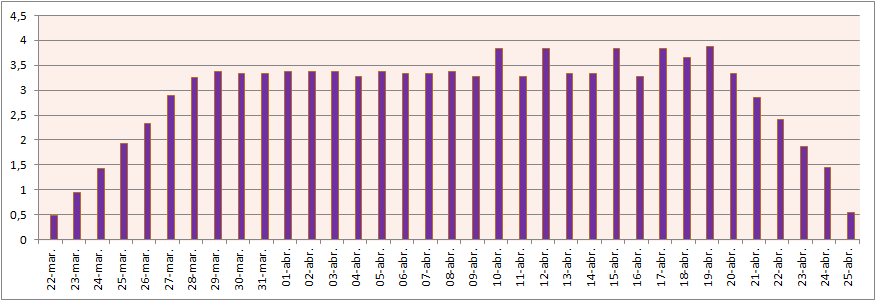
Entre las referidas fechas, ambas inclusive, 35 días. Lo primero (22 de Marzo, fecha más baja) sucedió en los años 1761 y 1818, no dándose durante todo el siglo XX y no volverá a darse hasta el año 2285; lo segundo (25 de Abril, fecha más alta) se dio en los años 1886 y 1943, volviendo a ocurrir este siglo, en el año 2038. No todos los días de este intervalo de 35 tienen la misma probabilidad. En general los valores próximas a los extremos (22 de marzo y 25 de abril tienen menos probabilidad) siendo el día 19 de abril el de máxima probabilidad con un 3,87 % según un estudio hecho en las pascuas de 5.700.000 años.
FÓRMULA PARA CALCULAR LA FIESTA DE LA PASCUA DE RESURRECCIÓN:
Como hemos dicho anteriormente la Pascua depende del movimiento lunar. Metón en el año 443 a J.C. descubrió la correspondencia casi exacta entre 19 años y 235 meses lunares o lunaciones medias, dato que se utiliza para el cálculo de la fecha de la Pascua de Resurrección. (1 año =365 días y 6 horas, es decir 365,25 días; 1 lunación= 29 días, 12 horas y 44 minutos, es decir 29,53 días)
235 lunaciones (meses lunares) tienen .....6939
días 16 horas 31 minutos
19 años trópicos verdaderos
tienen...........6939 días 14 horas 27 minutos
19 años julianos
de 365 ¼ días tienen........6939 días 18 horas 0
minutos
Han de pasar unos tres siglos para acumularse un día de error o diferencia.
Si anotamos la fecha en que ocurre la Luna llena pascual, no volveremos a encontrarla el mismo día en los 19 años consecutivos; pero en el 20mo caerá en el mismo día que en el primer año, o llevará solamente un día de diferencia, y a partir de aquí se repetirá la serie. El número áureo es el número de órden de un determinado año dentro del ciclo de Mentón. Varía de 1 a 19 y da así la manera de calcular, con exactitud suficiente para los fines religiosos, cuantos días después del equinoccio de primavera ocurre la Luna llena pascual. Los años suceden en orden del 1 al 19. Después del año aúreo 19 vuelve a empezar un nuevo ciclo.
La fórmula para calcular el número aúreo de un año es la siguiente:
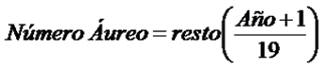
Por ejemplo el número aúreo del año 2016 es 3.
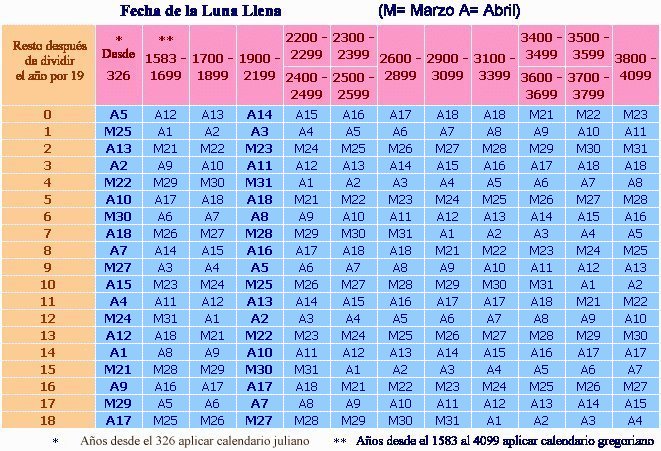
Para calcular el día que corresponde al domingo de pascua se requieren todavía otros datos: la denominada letra dominical (la letra que corresponde al primer domingo del año, si se designa el 1º de enero por la letra A y los días siguientes de la semana por B, C, D, E, F, G) y la epacta, que da la edad de la Luna, en días, el 1º de Enero, edad contada a partir del plenilunio.
Los cálculos de la Iglesia para determinar el domingo de pascua se efectúan con tablas de la Luna muy antiguas, de manera que se puede llegar a encontrar una semana de error respecto a los plenilunios calculados con las tablas modernas.
Existen varias fórmulas para calcular la fecha del Domingo de Pascua. Algunas son bastante complicadas y necesitan alguna corrección en algún año determinado.
La fórmula de Gauss es la que permite calcular con más sencillez la fecha del Domingo de Pascua:
PASCUA 22 + d + e (marzo) d + e - 9 (abril)
Las incógnitas de la fórmula (a, b , c, d, e) se calculan del modo siguiente:
- a: Resto de dividir un año determinado por 19
- b: Resto de dividir un año determinado por 4
- c: Resto de dividir un año determinado por 7
- d: Resto de la división de 19a + M por 30
- e: Resto de la división de 2b + 4c + 6d + N por 7
My N pueden calcularse directamente con la siguiente fórmula:
| Años | M | N |
| 326 - 1582 | 15 | 6 |
| 1583-1699 | 22 | 2 |
| 1700-1799 | 23 | 3 |
| 1800-1899 | 23 | 4 |
| 1900-2099 | 24 | 5 |
| 2100-2199 | 24 | 6 |
| 2200-2299 | 25 | 0 |
| 2300-2399 | 26 | 1 |
| 2400-2499 | 25 | 1 |
| 2500-2599 | 26 | 2 |
| 2600-2699 | 27 | 3 |
| 2700-2899 | 27 | 4 |
| 2900-2999 | 28 | 5 |
Calculando el valor de cada una de las variables para el año A en cuestión, la fecha del Domingo de Pascua será la siguiente:
Si d+e < 10 la fecha de Pascua de Resurrección será el día d + e +22 de marzo.
Si d+e >10, la fecha de Pascua de Resurrección será el día d + e - 9 de abril.
Casos raros o excepciones (a efectos de no coincidir las pascuas cristiana y judía)
Si obtenemos el 26 de abril con d=29, e=6, d+e-9=35-9=26 nos salimos del rango establecido, por lo que le deberemos restar 7 dias y la Pascua sería en ese caso particular el 19 de abril. Ejemplos de años: 2076- 1981
Si obtenemos el 25 de abril con d=28, e=6, d+e-9=34-9=25 y a>10 entonces la Pascua sería el 18 de abril.
Si le interesa puede descolgar el siguiente fichero en Excel que le calculará la Pascua y las fiestas movibles de cualquier año desde el año 1 al 9999 (Hay varios métodos diferentes).
Otra web de la pascua: https://www.catimenu.com/pascua-para-siempre.xlsm
También puede descolgar un fichero que le permitirá construir el calendario anual con las fiestas fijas y movibles con sólo introducir la cifra del año.
CALENDARIO CELEBRACIONES MÓVILES DE 2025
CALENDARI CELEBRACIONS DE 2025
QUADRE GENERAL DE FESTES I DIES NO LECTIUS
|
PRIMER SEMESTRE |
SEGON SEMESTRE |
|
- 1 gener: Cap d'Any -6 gener: Reis -18, 19 gener: Sant Antoni - Fira de la Trufa (no toca aquest any) - Prova ciclista: - 15 febrer: Carnestoltes a Catí - 1-2 març: Carnestoltes a Vinaròs - 3 març: Dilluns Magdalena - 5 març: Dimecres Cendra - 19 març: Sant Josep - : Prova ciclista - 17 abril: Dijous Sant - 18 abril: Divendres Sant - 19 d'abril: Fira d'abril - 20 abril: Diumenge Pasqua de Resurrecció - 21 d'abril: Dilluns romeria l'Avellà - 26 d'abril: Romería Sant Vicent - 28 d'abril: Dilluns Sant Vicent - 1 maig: Festa Treballador - 3, 4 maig: Romeria Sant Pere Castellfort - 5 maig: Festa Local - 17 maig: Primeres comunions a Catí |
- 1 juny: L'Ascensió - 7 juny: Cursa muntanya - 8 juny: Pasqua Pentecostés - 22 juny: - Corpus - 29 juny: Cor de Jesús (diumenge juny) - 26 juliol: Santa Anna - Fira Peraires (no previst) - 7 a 17 d'agost: Festes Majors 15, 16, 17 d'agost: Assumpció, Sant Roc i Sant Cristòfol - 11 setembre: Dia Marededéu de l'Avellà - 9 d'octubre: Diada autonòmica - 12 d'octubre: Dia del Pilar - 1 novembre: Tot Sants - 11 novembre: Sant Martí - 6 desembre: Dia Constitució - 8 desembre: Immaculada Concepció - 25 desembre: Nadal |
EJEMPLO PARA EL AÑO 2026:
| 2026 | a | Resto división 2024 por 19 | a=12 |
| b | Resto división 2024 por 4 | b=2 | |
| c | Resto división 2024 por 7 | c=3 | |
| d | Resto división 19a + M por 30 | d=12 | |
| e | Resto división 2b + 4c + 6d + N por 7 | e=2 |
M=24; N= 5
|
PASCUA 2026 |
22 + d + e (marzo) | 22+12+2 de marzo | de marzo (36-31)= 5 d'abril |
| d + e - 9 (abril) | 12 + 2- 9 de abril | 14- 9 de abril= 5 d'abril |
EJEMPLO PARA EL AÑO 2025:
| 2025 | a | Resto división 2024 por 19 | a=11 |
| b | Resto división 2024 por 4 | b=1 | |
| c | Resto división 2024 por 7 | c=2 | |
| d | Resto división 19a + M por 30 | d=23 | |
| e | Resto división 2b + 4c + 6d + N por 7 | e=6 |
M=24; N= 5
|
PASCUA 2025 |
22 + d + e (marzo) | 22+23+6 de marzo | 51 de marzo (51-31)= 20 d'abril |
| d + e - 9 (abril) | 23+ 6 -9 de abril | 29- 9 de abril= 20 d'abril |
EJEMPLO PARA EL AÑO 2024:
| 2024 | a | Resto división 2024 por 19 | a=10 |
| b | Resto división 2024 por 4 | b=0 | |
| c | Resto división 2024 por 7 | c=1 | |
| d | Resto división 19a + M por 30 | d=4 | |
| e | Resto división 2b + 4c + 6d + N por 7 | e=5 |
M=24; N= 5
|
PASCUA 2024 |
22 + d + e (marzo) | 22+4+5 de marzo | 31 de marzo |
| d + e - 9 (abril) | 4+ 5-9 de abril | 0 de abril= 31 de marzo |
RESTO DE FIESTAS MOVIBLES DEL AÑO:
Una vez establecida la fiesta del Domingo de Pascua de Resurrección pueden establecerse fácilmente el resto de las fiestas movibles del año. Algunas de las cuales son:
| Domingo de Septuagésima | 17 días antes del Miércoles de Ceniza |
| Semana de Carnaval | La semana anterior al Miércoles de Ceniza |
| Miércoles de Ceniza (Inicio cuaresma) | 46 (47 en año bisiesto) días antes del Domingo de Pascua |
| Domingo de Ramos | 7 días antes del Domingo de Pascua |
| Jueves Santo | 3 días antes del Domingo de Pascua |
| Viernes Santo | 2 días antes del domingo de Pascua. |
| Domingo de Pascua de Resurrección | Principal fiesta cristiana de la que dependen las demás |
| Lunes de Pascua | 1 dia después del Domingo de Pascua (Romería) |
| Lunes de San Vicente | 8 días después del Domingo de Pascua |
| Domingo de Ascensión (antes jueves) | 42 días después del domingo de Pascua. |
| Domingo de Pascua de Pentecostés | 49 días después del domingo de Pascua |
| Domingo Santísima Trinidad | 56 días después del domingo de Pascua |
| Domingo de Corpus Christi (antes jueves) | 63 días después del domingo de Pascua |
| Domingo Sagrado Corazón de Jesús | Un domingo del mes de junio. |
| 1er. Domingo de Adviento | Domingo más próximo al 30 de diciembre (27 nov a 3 dic). |
Comuniones: Uno de los domingos (Ascensión o Pascua de Pentecostés)
|
|
|
Domingo de Ramos- 17 de abril de 2011 (Catí) |
PASCUAS DE RESURRECCIÓN DESDE EL AÑO 2000 AL 2049:
| AÑO | PASCUA | AÑO | PASCUA | AÑO | PASCUA | AÑO | PASCUA | AÑO | PASCUA |
| 2000 | 23 abril | 2010 | 4 abril | 2020 | 12 abril | 2030 | 21 abril | 2040 | 1 abril |
| 2001 | 15 abril | 2011 | 24 abril | 2021 | 4 abril | 2031 | 13 abril | 2041 | 21 abril |
| 2002 | 31 marzo | 2012 | 8 abril | 2022 | 17 abril | 2032 | 28 marzo | 2042 | 6 abril |
| 2003 | 20 abril | 2013 | 31 marzo | 2023 | 9 abril | 2033 | 17 abril | 2043 | 29 marzo |
| 2004 | 11 abril | 2014 | 20 abril | 2024 | 31 marzo | 2034 | 9 abril | 2044 | 17 abril |
| 2005 | 27 marzo | 2015 | 5 abril | 2025 | 20 abril | 2035 | 25 marzo | 2045 | 9 abril |
| 2006 | 16 abril | 2016 | 27 marzo | 2026 | 5 abril | 2036 | 13 abril | 2046 | 25 marzo |
| 2007 | 8 abril | 2017 | 16 abril | 2027 | 28 marzo | 2037 | 5 abril | 2047 | 14 abril |
| 2008 | 23 marzo | 2018 | 1 abril | 2028 | 16 abril | 2038 | 25 abril | 2048 | 5 abril |
| 2009 | 12 abril | 2019 | 21 abril | 2029 | 1 abril | 2039 | 10 abril | 2049 | 18 abril |
OTROS DATOS DE INTERÉS:
El calendario juliano fue introducido por Julio Caesar el año 45 AJC sustituyendo a los calendarios lunares vigentes hasta entonces. Establecía un calendario solar con una duración del año de 365.25 días pues intercalaba un año bisiesto cada 4 años. Se cometía un error de 7,5 días por milenio.
- El calendario actual o gregoriano obedece a la reforma del calendario juliano que ordenó el Papa Gregorio XIII en 1582. La duración del año juliano era mayor que la duración real del año que es de 365.2422 días por lo que provocaba un adelanto progresivo en el calendario de la fecha en que comienzan las estaciones. Como la Pascua se regía por un equinoccio fijado arbitrariamente el 21 de Marzo, con el transcurso del tiempo caía más y más tarde amenazando en caer en verano. Fue precisamente el problema de la fecha de la Pascua lo que originó en 1582 por Gregorio XII, la reforma del calendario que substancialmente intenta fijar el equinoccio de Primavera en la fecha del 21 de Marzo fijada por el Concilio de Nicea. Fue el 4 de octubre de 1582 cuando se corrigió el calendario eliminándose 10 días de error y saltando directamente del 4 al 15 de octubre de dicho año.
El calendario gregoriano es un calendario solar, es decir, basado en la duración de un año solar (365, 242 días). Los años duran 365 días y cada 4 años se añade un día más para corregir la pérdida aproximada de un día. De los años seculares sólo son bisiestos los que son múltiplos de 400.
La mayoría de los países adoptaron rápidamente el calendario gregoriano: Francia, Italia y España (1582), Gran Bretaña (1752), Japón (1863), Rusia (1918), Rumania y Grecia (1924), Turquía (1927).
- Los calendarios luni-solares como el israelita, chino, griego antiguo, indio, maya, mongol.. dan al año la misma duración pero los meses siguen aproximadamente las lunaciones. Tienen un mes variable que permite realizar ciertos ajustes de modo que al cabo de un cierto ciclo el año comience en las mismas circunstancias astronómicas.
En el calendarío judío, por ejemplo, ya adoptado por los israelitas antes de Moisés, el año tiene ordinariamente doce meses (lunares) de veintinueve o treinta días, pero cada dos o tres años (más precisamente, en siete años de cada diecinueve: los números tres, seis, ocho, once, catorce, diecisiete y diecinueve en su versión actual) se le agrega otro mes al final del año, llamado adar sheni o segundo adar, para mantener la coincidencia del año lunar con el solar. Así, los años comunes tienen doce meses (353, 354 o 355 días) y los extraordinarios (o años embolismáticos) resultan de trece (383, 384 o 385 días). Cada diecinueve años, período llamado ciclo metónico durante el cual se producen 235 lunaciones, los calendarios lunar y solar se reencuentran (con una diferencia del orden de las dos horas). El ciclo metónico o de Metón se llama así por el astrónomo ateniense de ese nombre, que vivió en el siglo de Pericles (el V a.C.),
| AÑO JUDIO 5764 | AÑO (2003-2004) | AÑO JUDIO 5765* | AÑO (2004-2005) |
| 1.-Tishrei (30) | 27 Septiembre-26 Octubre | 1.-Tishrei (30) | 16 Septiembre-15 Octubre |
| 2.- Cheshvan (30) | 27 Octubre-25 Noviembre | 2.- Cheshvan (29) | 16 Octubre-13 Noviembre |
| 3.-Kislev (30) | 28 Noviembre- 25 Diciembre | 3.-Kislev (29) | 14 Noviembre-12 Diciembre |
| 4.-Tevet (29) | 26 Diciembre- 23 Enero | 4.-Tevet (29) | 13 Diciembre-10 Enero |
| 5.- Shvat (30) | 24 Enero- 22 Febrero | 5.- Shvat (30) | 11 Enero- 9 Febrero |
| 6.-Adar1 (29) | 23 Febrero- 22 Marzo | 6.-Adar1 (30) | 10 Febrero-11 Marzo |
| 7.- Adar2 (29)* | 12 Marzo- 9 Abril | ||
| 7.- Nisan (30) | 23- Marzo-21 Abril | 8.- Nisan (30) | 10 Abril- 9 Mayo |
| 8.- Iyyar (29) | 22 Abril-20 Mayo | 9.- Iyyar (29) | 10 Mayo-7 Junio |
| 9.- Sivan (30) | 21 Mayo- 19 Junio | 10.- Sivan (30) | 8 Junio- 7 Julio |
| 10.- Tamuz (29) | 20 Junio- 18 Julio | 11.- Tamuz (29) | 8 Julio- 5 Agosto |
| 11.- Av (30) | 19 Julio-17 Agosto | 12.- Av (30) | 6 Agosto- 4 Septiembre |
| 12.- Elul (29) | 18 Agosto- 15 Septiembre | 13.- Elul (29) | 5 Septiembre- 3 Octubre |
* Año embolismático: Añade el mes Adar2
El año judío comienza en el mes de septiembre del calendario gregoriano. Hay una diferencia de 3760 años entre un año judío y su correspondiente gregoriano. Así por ejemplo el año judío 5764 comenzó el día 27-09-2003 y terminó el día 15-09- 2004. El año siguiente 5765 comenzó el día 16-09-2003. Si observamos los inicios de los dos años 27-09 y 16-09 se observa un retraso de 11 días. Este retraso al cabo de dos o tres años se corrige (año embolismático), añadiendo un mes de 29 días, tal como puede observarse en la tabla en el año 5765.
Por lo anterior, cualquier festividad judía, como la Pascua, que tiene lugar el 15 del mes Nisán del calendario judío, tiene un comportamiento curioso si se analiza en qué día del calendario occidental cae: en ciertos años la fiesta se aproxima once o doce días a principio de año con relación al año precedente, pero en otros tiene lugar casi veinte días más tarde, bien entrado el mes de abril. Como se podrá apreciar por lo explicado, hace lo primero en doce años de los diecinueve del ciclo de Metón, y lo segundo en los otros siete (en los años judíos embolísmicos).
Los años embolísmicos más próximos al actual del calendario judío son:
| Año ciclo Metón | 3 | 6 | 8 | 11 | 14 | 17 | 19 | 3 | 6 | 8 | 11 | 14 | 17 | 19 |
| Año embol. judío | 5741 | 5744 | 5746 | 5749 | 5752 | 5755 | 5757 | 5760 | 5763 | 5765 | 5768 | 5771 | 5774 | 5776 |
| Año gregoriano | 80-81 | 83-84 | 85-86 | 88-89 | 91-92 | 94-95 | 96-97 | 99-00 | 02-03 | 04-05 | 07-08 | 10-11 | 13-14 | 15-16 |
- El calendario lunar, como el musulmán, se basa exclusivamente en la duración del mes lunar. Los años son de 12 meses de 29 o 30 días (año de 354 o 355 días). Así 33 años musulmanes equivalen a 32 años naturales. En este calendario no hay correcciones para que los meses lunares coincidan con el ciclo solar y no se desplacen con relación a las estaciones del año. Esto ocasiona que una celebración árabe como el Ramadán, el mes de ayuno, se va retrasando a lo largo del año solar y puede caer en cualquier momento del año occidental (se desplaza un año completo a lo largo de 30). Ahora el Ramadán cae en el invierno, pero dentro de 15 años caerá en el verano.
CALENDARIO PERPETUO:
TABLA I - AÑOS
|
CALENDARIO PERPETUO DE MORET
PARTE DE LA CIFRA DEL AÑO QUE EXPRESA LAS CENTENAS (siglo) |
00(d) | 01 | 02 | 03 | 04 | 05 |
INSTRUCCIONES: 1º) Buscar en la tabla I (años) el número situado en la intersección de la línea que contiene las cifras del siglo y la columna que contiene las del año. 2º) Tomar en la columna exterior de la tabla II (meses), el número así encontrado y buscar el que se encuentra en la intersección de esta línea y la columna del mes. En los años bisiestos, tomar los meses de enero y febrero marcados con la letra B. 3º) Volver a tomar en la columna exterior de la tabla III (Días del mes) el nuevo número así encontrado. En la intersección de esta línea y la columna de los días del mes se encuentra el día buscado.
EJEMPLO: ¿Qué día fue el 20 de julio de 1969? (Día llegada del primer hombre a la Luna) TABLA I Línea 19; Columna 69- Intersección, cifra encontrada: 4 TABLA II: Línea 4 ; Columna julio. cifra encontrada: 3 TABLA III: Línea 3; Columna 20, día buscado DOMINGO
NOTAS: (b): Hasta el 4-10-1582 (c): Desde el 15-10-1582 (Del 5 al 14-10-1582 no están especificadas) (d): Los años seculares no son bisiestos más que cuando son divisibles por 400. (e): Abreviaturas: m: martes ; M: miércoles
| |||||
| 06 | 07 | 08 | 09 | 10 | 11 | |||||||
| 12 | 13 | 14 | 15 | 16 | ||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||||||
| 23 | 24 | 25 | 26 | 27 | ||||||||
| 28 | 29 | 30 | 31 | 32 | 33 | |||||||
| 34 | 35 | 36 | 37 | 38 | 39 | |||||||
| 40 | 41 | 42 | 43 | 44 | ||||||||
| 45 | 46 | 47 | 48 | 49 | 50 | |||||||
| 51 | 52 | 53 | 54 | 55 | ||||||||
| 56 | 57 | 58 | 59 | 60 | 61 | |||||||
| 62 | 63 | 64 | 65 | 66 | 67 | |||||||
| 68 | 69 | 70 | 71 | 72 | ||||||||
| 73 | 74 | 75 | 76 | 77 | 78 | |||||||
| 79 | 80 | 81 | 82 | 83 | ||||||||
| 84 | 85 | 86 | 87 | 88 | 89 | |||||||
| 90 | 91 | 92 | 93 | 94 | 95 | |||||||
| 96 | 97 | 98 | 99 | |||||||||
| 0 | 7 | 14 | 17 | 21 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 8 | 15(b) | 5 | 6 | 0 | 1 | 2 | 3 | 4 | |||
| 2 | 9 | 18 | 22 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | ||
| 3 | 10 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | ||||
| 4 | 11 | 15(c) | 19 | 23 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | |
| 5 | 12 | 16 | 20 | 24 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | |
| 6 | 13 | 0 | 1 | 2 | 3 | 4 | 5 | bgColor=#ff8000>6 | ||||
|
TABLA II |
TABLA III | |||||||||||||||
|
MESES (d) |
DÍAS DEL MES(e) | |||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||||
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||
| Febrero | Septiembre | Abril | 15 | 16 | 17 | 18 | 19 | 20 | 21 | |||||||
| Mayo | Agosto | Marzo | Junio | Diciembre | Julio | Enero | 22 | 23 | 24 | 25 | 26 | 27 | 28 | |||
| Febrero B | Noviembre. | Enero B | Octubre | 29 | 30 | 31 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 1 | D | L | m | M | J | V | S | |
| 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 2 | L | m | M | J | V | S | D | |
| 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 3 | m | M | J | V | S | D | L | |
| 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 4 | M | J | V | S | D | L | m | |
| 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 5 | J | V | S | D | L | m | M | |
| 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 6 | V | S | D | L | m | M | J | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 0 | S | D | L | m | M | J | V | |
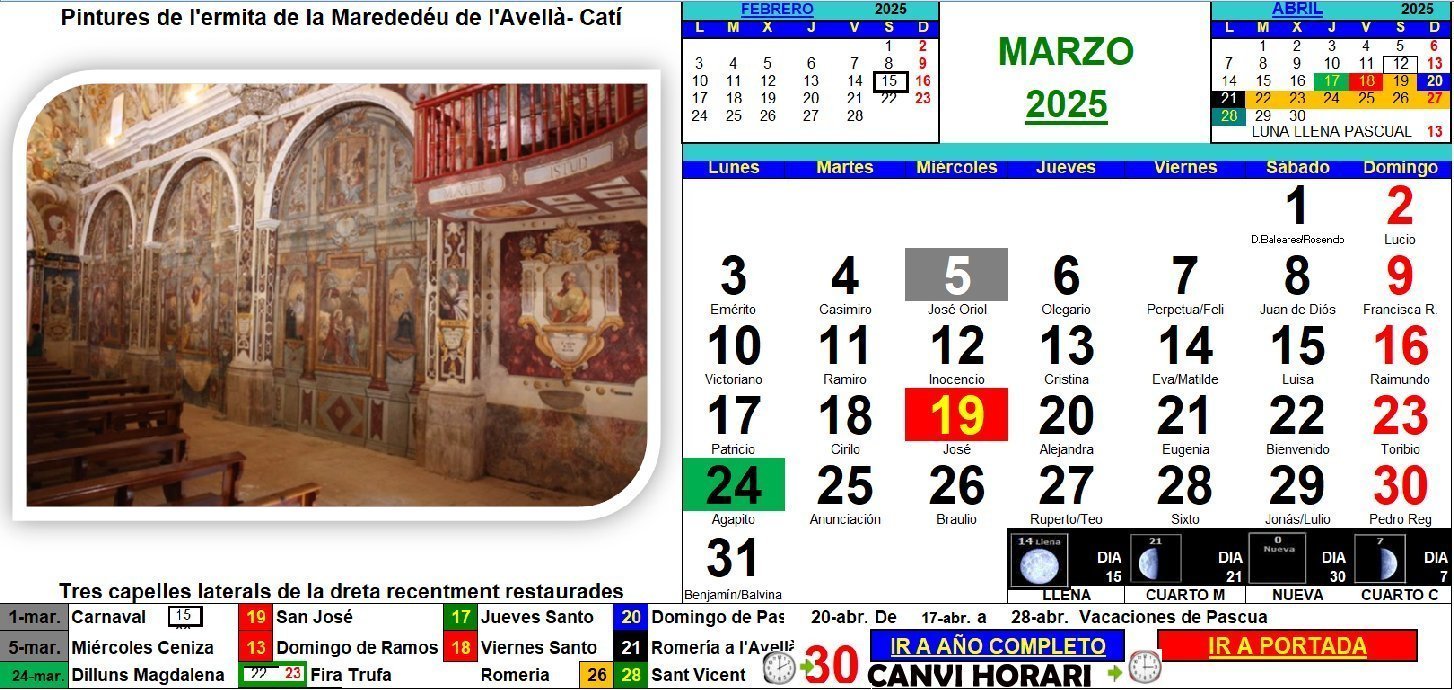
Podemos ver juntos los meses de marzo, abril y mayo de 2024 en los siguientes gráficos:


© Páginas creadas por Joaquim Carbó Miralles , 1998
Texto: Enciclopedia Larousse
Última actualitzación: 18/03/2025